//Easing Tutorial : Keith Peters : Bit-101.com

//Easing Tutorial
© Keith Peters [Bit-101.com]

This tutorial is going to go over the subject of "easing." The question is often asked, "How do I make an object go towards a particular point, but slow down as it approaches, smoothly sliding into place?" This is called easing, and it is pretty easy to do once you get the hang of it. It is used to create realistic movement effects. Imagine you are driving along at 60 miles an hour, going home. You don't keep going 60 until you are in your driveway and suddenly stop cold. You slow down to 40, then 25, 15, 10, 6, 4, 2, 1 then stop. Actually, you would start driving the same way, gradually building speed. This would be easing out. I'm just going to cover easing in with this tutorial, but that will go a long way.

Easing is basically one simple formula that can be adjusted to create the exact effect you want. Once you've got it down, you might see uses for it other than just motion, such as adjusting the rotation of an object, the scale, the _alpha or even changing colors. Any situation where you would want to have something gradually adjust to a specific state.

OK, so let's look at the physics involve.

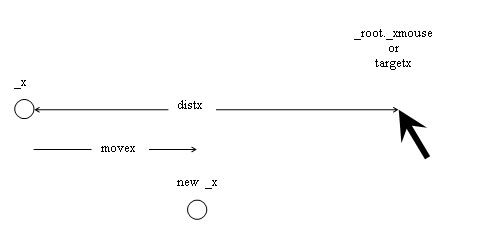
You are at a certain place and you want to ease in to another place.

First let's do it all in on jump. We'll create an object and situation we can work with for the rest of this tutorial. Create some shape of your own choice, convert it to a movie clip and put the following code on it:

onClipEvent(load){ _x=0; _y=0; } onClipEvent(mouseDown){ targetx=_root._xmouse; targety=_root._ymouse; } onClipEvent(enterFrame){ _x=targetx; _y=targety; }

What this does is:
1. First locates the object at 0, 0.
2. When the mouse button is pressed, the coordinates of the mouse are stored in targetx and targety.
3. It changes the coordinates of the movie clip to targetx and targety.

Test it out. Wherever the object is, when you click the mouse, the object appears under the mouse cursor. It does this instantly, in one frame.

OK. Now, let's make the first ease. Here is the theory:

1. We know where we are.
2. We know where we want to go.
3. We can figure out the distance from here to there.
4. We are going to move exactly one half of that distance.
5. From our new position…

1. We again know where we are.
2. Where we are going is still the same.
3. We can compute this new distance.
4. We will move exactly one half of that distance.
5. Again, start over at 1.

Each time through the loop, we are moving less and less. So we will start out rather fast, and get slower and slower as we approach the target. Theoretically, we will never actually reach the target, since no matter how close we get, we will always cut that distance in half on the next step. But when you are 1/100th of a pixel away from something, you can safely say you have arrived there!

So, translating this into Actionscript, I will first make each calculation a separate line of code for clarity's sake. Later I'll show you the shorthand formula which you should burn into your brain. Also, we'll start out with just _x movement for simplicity. Then we just add the same lines, substituting _y for _x.

Here it is:

onClipEvent(load){
_x=0; _y=200; }

onClipEvent(mouseDown){
targetx=_root._xmouse; }
onClipEvent(enterFrame){

distx=targetx-_x;
movex=distx/2;

_x+=movex; }

(note: Some people have asked about this += thing. It is the add and assign operator. It takes the variable, adds a value to it and assigns the result back to the variable. i.e. _x+=movex is the same as _x=_x+movex )

Translating to our original steps:

1. Where we are is _x.
2. Where we want to go is targetx.
3. The distance is targetx-_x or distx.
4. Half of distx is distx/2 which we assign to movex and then add that to _x : _x+=movex
5. The next frame starts again at 1.

Test that. Now when you click the mouse, the object should not just jump to that point, but slide there smoothly. Oh, of course at this stage, it's just going to move horizontally since we didn't do anything with _y yet. Before we do that, let's compact the code and get rid of some of the extra variables. Hopefully you can follow along with the changes here:

onClipEvent(load){ _x=0; _y=200; } onClipEvent(mouseDown){ targetx=_root._xmouse; } onClipEvent(enterFrame){ _x+=(targetx-_x)/2; }

Now, in one line: _x+=(targetx-_x)/2; we are finding the distance, dividing by 2 and adding it to _x.

If you are still following along at this point, it is safe to add your code for _y. Don't forget the targety in the first block of code:

onClipEvent(load){ _x=0; _y=0; } onClipEvent(mouseDown){ targetx=_root._xmouse; targety=_root._ymouse; } onClipEvent(enterFrame){ _x+=(targetx-_x)/2; _y+=(targety-_y)/2; }

Test that and the object should slide in to the exact point you clicked. Pretty cool so far, but we are not done yet.

Whenever I see a number written into code, like that "2" there, it bothers me. I almost always like to replace them with a variable, especially if there is a chance you might want to change it at some point (which we are about to do). Here is the final code we will be using:

onClipEvent(load){ _x=0; _y=0; speed=2; } onClipEvent(mouseDown){ targetx=_root._xmouse; targety=_root._ymouse; } onClipEvent(enterFrame){ _x+=(targetx-_x)/speed; _y+=(targety-_y)/speed; }

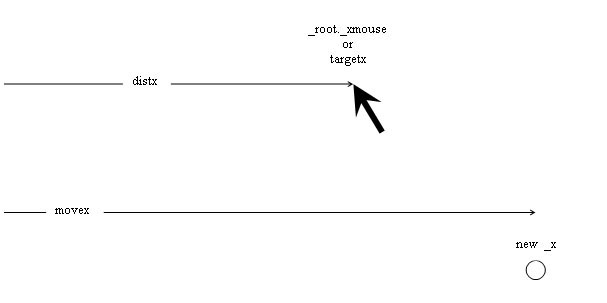
Now the obvious thing is to play around with the speed variable. If you set it to 1, you will see that the file behaves exactly like the first file we made. The object will jump to the target location in one step. The higher you set the speed variable, the slower it will travel.

Say we set it to 10. It will calculate the distance to travel and only travel 1/10 of that distance. Then it will travel 1/10 of the remaining distance. It will take a long time to get there. You can adjust this variable to create the exact effect you are looking for.

Now, one last bonus. Try setting the speed variable as a fraction between 0.5 and 1.0. I find that around 0.6 gives a nice effect. This creates an elastic, bouncing effect. You are now dividing the distance by a fraction. This makes the object move more than the distance. So it overshoots the target and goes beyond it. Then it bounces back the other way, again overshooting, but not as much. And so on, until it is virtually still.

That's about all there is to easing. Actually, there are more complex formulas that can be used based on other various mathematical functions but I think you will find that this formula is a very quick and simple way of achieving great results 99% of the time. As you get used to it, experiment using it on other properties of movie clips - _rotation, _alpha, scale, etc. In closing, I'll state the generic form of the formula that you should memorize:

NextStep = (WhereYouWantToGo - WhereYouAre) / Speed;

Usually this ends up as:

property = (target - property)/speed;

I hope you can take what I did here and evolve it into something even more interesting. If you do, please show me. Good luck. If you add any comments or additions to the end of this document, please send me a copy too. Thanks.

Keith Peters
kp@bit-101.com

Comments or additions by others:
(please include name, e-mail and date)