BIT-101

Simplifying Paths

Background

About a year ago I made a post about Evenly Placed Points on Bézier Curves. I’ve found that code to be enormously useful. In fact, recently, I expanded on this concept, so I can go from a list of points that create a path like this…

to a path made of piecewise quadratic Bézier curves like this…

to a path of points that recreates the curve directly like this…

The second two images may look the same, but one is drawn using quadratic Bézier curves and the other is drawn with a series of points with straight line segments between them. In fact, here’s that image drawn again, with only points, not lines. You’ll have to look pretty closely to see the points.

As described in the above-mentioned post, the latter is useful for interpolating along the curve, or placing items on the curve, or finding a point on the curve that it closest to some external point, and other things. The functionality I have now lets me go from the list of points in image 1 the the expanded list of points forming the curves in image 3, in one shot.

An example is this piece I did a couple of days ago.

The circles traveling on the edge of the curve are uniformly distributed along that curve and they need to know the exact position of that curve at any point. This would be pretty tough with regular Bézier curves, but with uniformly interpolated points along the curve it’s much easier.

The Problem

Since my function takes an unknown number of points in unknown positions and forms an unknown number of quadratic Bézier curves of unknown length, it’s impossible to know how many points to assign to each curve individually. That is, how many small segments to break each curve into so it closely follows the shape of the curve. Through trial and error I’ve found that around 50 points virtually always does a completely suitable job. Fewer than that, and in some complex curves you wind up with sharp corners here and there. So I hard-coded 50 into the function.

And in general this has been great but I know in some cases I’m winding up with many, many more points than I really need. If I have just 6 points in my original list, that winds up with 6 curves and 300 points in the final path. Again, look at the previous image with the curve rendered only in points. Many of the points are so tightly packed you can barely see them individually.

So rather than trying to get the magic number of points up front, I started thinking about how I could simplify the path after the fact. Remove the extraneous points, keep the necessary ones.

The Solution

In transparency, I’ve done this kind of thing before in Flash, probably close to a couple of decades ago. I remembered what I did then and tried to recreate it. To pretty good success in fact.

The concept is pretty simple. I loop through my point list, looking at groups of three consecutive points, points[0], points[1] and points[2] for example. Call them pA, pB and pC. Then I test if these three points are co-linear. In other words, do they fall on the same line? If so, then pB isn’t adding anything to the curve at all. I could just draw a line from pA to pC, ignoring pB altogether and you wouldn’t know the difference. So I remove pB from the list and carry on through the rest of the list.

Something like this:

function simplify(points) {
    for (i = 0; i < points.length - 2; i++) {
        pA = points[i]
        pB = points[i+1]
        pC = points[i+2]
        if (colinear(pA, pB, pC)) {
            points.remove(pB)
        }
    }
}

Obviously, that’ pseudocode, and altering a list while iterating through it can get you in trouble. It all worked out for me the way I set it up in Go, but I’ll leave it to you to figure out the best way to cull out those middle co-linear points in your language and framework.

Now of course, it’s impossibly rare that you’ll ever find three dynamically generated points that are exactly co-linear, so we’ll allow a little leeway. We’ll actually be saying, are these points close enough to being co-linear?

So how do you tell if three points are co-linear? Well, there are different ways to go about this. The most obvious and direct is to compare the slope of the line from pA to pB to the slope between pB and pC. That would look something like:

function colinear(pA, pB, pC, threshold) {
    m0 = (pB.y - pA.y) / (pB.x - pA.x)
    m1 = (pC.y - pB.y) / (pC.x - pB.x)
    diff = abs(m1-m0)
    return diff < threshold
}

Now you can adjust your threshold value so you’re removing the most points possible, but your curve isn’t starting to get chunky. I find that a threshold of around 0.1 gives pretty good results. This means that if the two slopes differ by less than 0.1 you can remove the middle point.

Visually, this image might help:

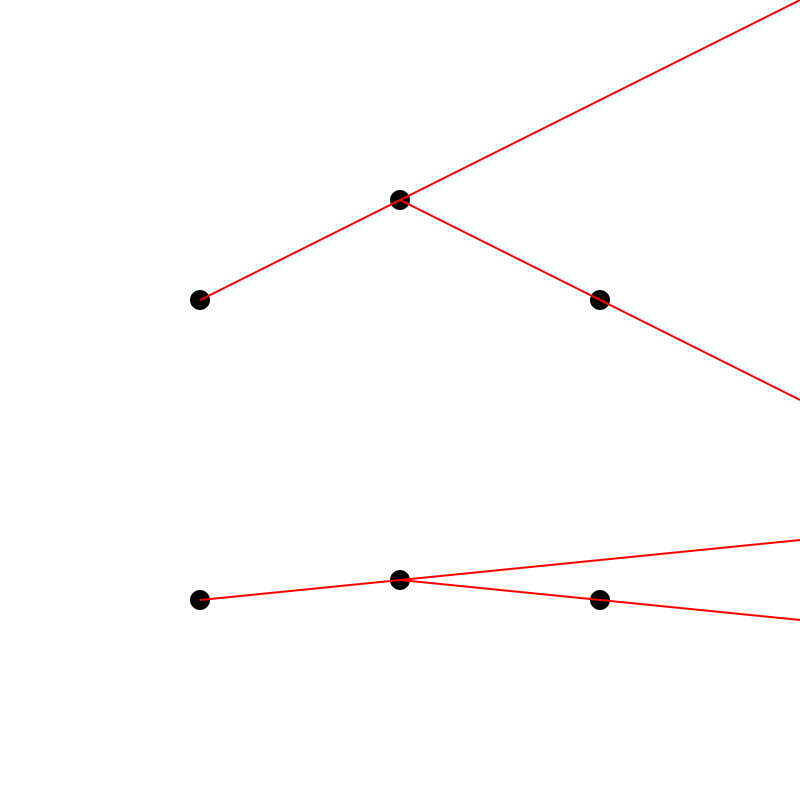
In the top image, the slop from the first to second point is quite different than the slope from the second to the third. These are very far from co-linear.

In the bottom image, the slopes are pretty similar. This is just a visual example, but you might be able to say this is close enough to co-linear.

But I found I got a lot better results with a different method.

Alternate method

In my library I have a Segment object, which is formed by two points. And I have a Segment.distanceTo(point) function that you can pass a point into and it gives you back the distance from that point to the segment. I make a segment with pA and pC and get the distance from pB to that segment. It’s something like this:

function colinear(pA, pB, pC, threshold) {
    segment = new Segment(pA, pC)
    dist = segment.distanceTo(pB)
    return distance < threshold
}

Here, I find a threshold of about 0.25 gives good results. In this case it means pB needs to be less than a quarter of a pixel from the segment formed by pA and pB in order to be removed. That’s pretty close to co-linear.

Here you can see the first and third points joined by a segment (in black) and the distance from the middle point to that segment in red. In this case, it’s pretty close to the segment and might be considered co-linear.

Btw, you can find my Segment object here: https://codeberg.org/bit101/bitlib/src/branch/main/geom/segment.go

For whatever reason, with this method I can remove a lot more points and still have a much smoother, more accurate curve than I can using the slope method.

My theory is that with the slope method, you can have a sequence of points that are very close together. The slopes might differ more than your threshold, so the middle point doesn’t get removed. But because the distances are so small, that middle point is visually co-linear - maybe only a small fraction of a pixel away. It should be removed.

Again a visual might help.

Consider this a very zoomed in view of three consecutive points. The slopes between the two pairs differs by a good amount, but if you consider that each circle is one pixel in diameter, it’s only off by a small fraction of a single pixel. If you zoomed out, you’d barely see this.

So you wind up with not as many points being removed. But if you crank up the threshold to catch those close-up points, you wind up removing too many points in areas where the points are further away and things get chunky there.

The distance-to-segment method is much more aggressive on closely spaced points, where you’re safe to remove more, but more lenient on larger curves with more space, where you want to keep points for accuracy.

That’s my theory anyway.

Iteration

If you do well here, you could end up removing a good number of points. Maybe even half, depending on the state of your list. But you might be able to do better. Run it again and you might be able to remove a few more. And again, and maybe again a couple more times. Rather than manually calling it a bunch of times, you can add an iteration parameter to your simplify function. I’ll also throw in a threshold parameter.

function simplify(points, threshold, iter) {
    for (j = 0; j < iter; j++ ) {
        for (i = 0; i < points.length - 2; i++) {
            pA = points[i]
            pB = points[i+1]
            pC = points[i+2]
            if (colinear(pA, pB, pC, threshold)) {
                points.remove(pB)
            }
        }
    }
}

I’ve found that on a fairly complex curve, with the distance-to-segment method and a threshold of 0.1, five iterations gets down to the minimal number of points. Anyway, this method gives you full control. But maybe you want something simpler that just works pretty good most of the time.

Auto-simplify

I created another method called autosimplify. This hard-codes the 0.25 and intelligently iterates as much as it needs to.

It does this by keeping track of the number of points before and after each iteration. If it’s the same, then it’s stopped removing any points. You’re done. If it removed any, then it will try again and see if it can removed more.

function autosimplify() {
    count = points.length
    while true {
        for (i = 0; i < points.length - 2; i++) {
            pA = points[i]
            pB = points[i+1]
            pC = points[i+2]
            if (colinear(pA, pB, pC, 0.25)) { // hard-coded threshold
                points.remove(pB)
            }
        }
        if (points.length == count) {
            // we didn't remove anything this time. done.
            return
        } else {
            // we removed something. keep track for next time.
            count = points.length
        }
    }
}

Stress Test

To show off the results - both in quality and in point removal, I created this stress test. It starts off with 50 moving randomized points. This creates 50 internal curves with 50 points, for a total of 2,500 points in the final curve. (2,501 actually, since I add an extra one in there to close the loop for… reasons.) This original path is drawn in blue. Then I run the autosimplify function as described above, and shift the result over 10 pixels. In the center, I print the number of original and simplified points.

To my eyes, there is little or no difference. And the numbers don’t lie. Average reduction is 80%.

Summary

The concept here is, start with more points than you probably need. Then, intelligently cull out the ones you don’t need.

I’m sure there are improvements that can be made here. Maybe a more dynamic colinear method that takes into account not only the slope but the distance. I’m sure this will see some improvements over time.

Comments? Best way to shout at me is on Mastodon

Or share this post directly on Mastodon