BIT-101

Questioning Sierpinski

I had a stray thought about the Sierpinski triangle this morning. A different way of looking at it. I’m under no illusions that I’m the first one to try this idea out, but in the 35+ years I’ve been obsessed with fractals, chaos and strange attractors, I’ve never run across any examples like this, which is surprising, because it’s a very simple idea.

I tried the idea out and found it created some very nice patterns, some very Sierpinski-like, and some quite unexpected. So I figured I’d share.

Background

A quick refresher on the Sierpinski triangle. I assume you all know how it works, so I’ll be brief.

You take an equilateral triangle, split it into four equal triangles and remove the center one.

Then you do the same for the three remaining triangles.

And so on, down to the level where the scale is so small you’re not seeing the results anymore.

You know all this.

Question Authority

My stray thought this morning was, “why do we always remove the center triangle?”

What happens if we start removing other triangles instead?

Let’s try it. We’ll remove the top triangle.

Note: there’s some artifacting here - you can see a faint line between each rendered triangle. Though not initially intended, it kind of works to my advantage, letting you see the different triangles to some degree.

OK, fine. Now when we go to the next level, we have that center triangle still. But when we split that up, it’s not going to have a “top triangle”. Well, we can just say that triangle was rotated 180 degrees, so we rotate the algorithm by 180 degrees, and remove the bottom triangle. Now level two looks like this.

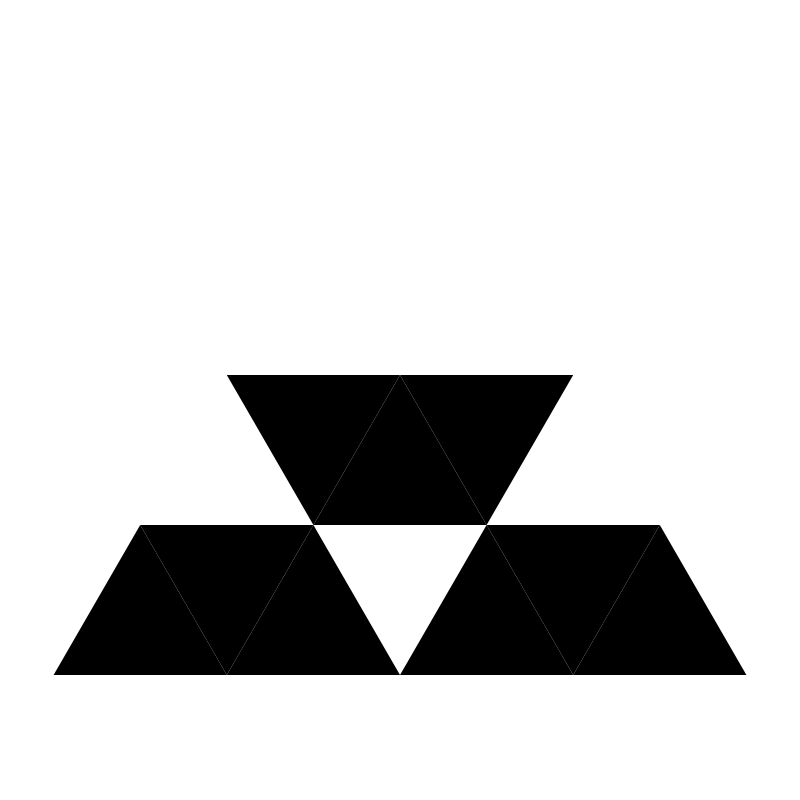
The next level…

And all the way down (visibly anyway)

Now what happens if instead or removing the top triangle, we always remove the bottom right?

Or the bottom left?

It’s just the same thing, rotated. Makes sense. 

So far, it’s still vaguely Sierpinski-ish, but… there’s a lot of other stuff going on there.

Keep Questioning

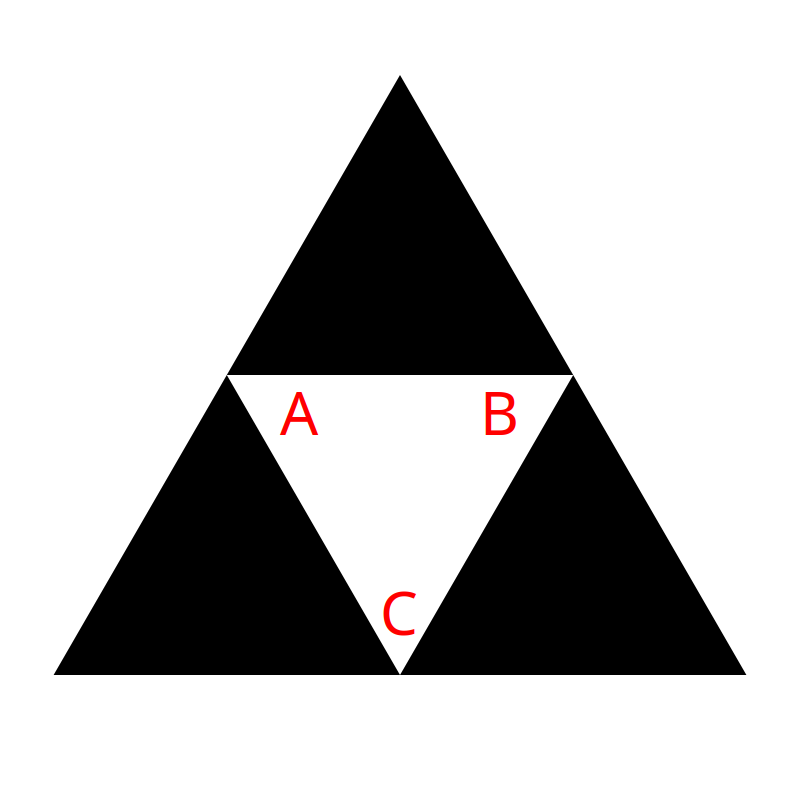
We made an easy assumption there when we decided how to deal with the upside-down center triangle. We said it was just rotated 180 degrees. But it could have been rotated 60 degrees to the left or 60 degrees to the right and also appear as an “upside down” triangle. Now our “top”, “bottom left”, bottom right” terminology starts to get confusing. So let’s label the different triangles A, B, C and D. 

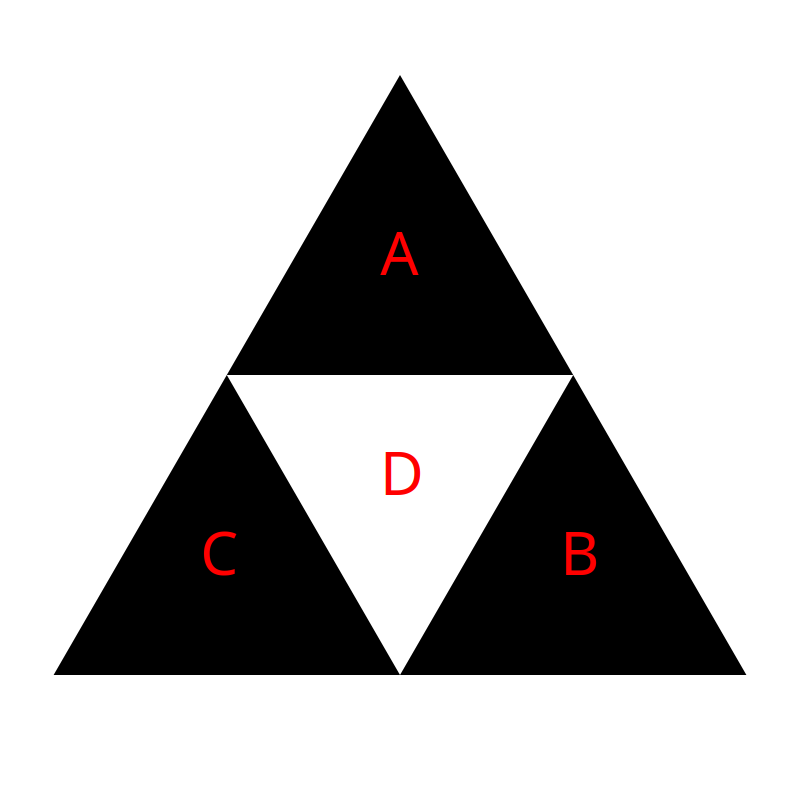
In the conventional Sierpinski, we always remove D. So how we rotate the center triangle doesn’t matter. When we’re removing A, B or C, it starts to make a big difference. We have three possibilities, with three different outcomes. We can rotate the center triangle so that A is at the bottom, or B is at the bottom or C is at the bottom. 

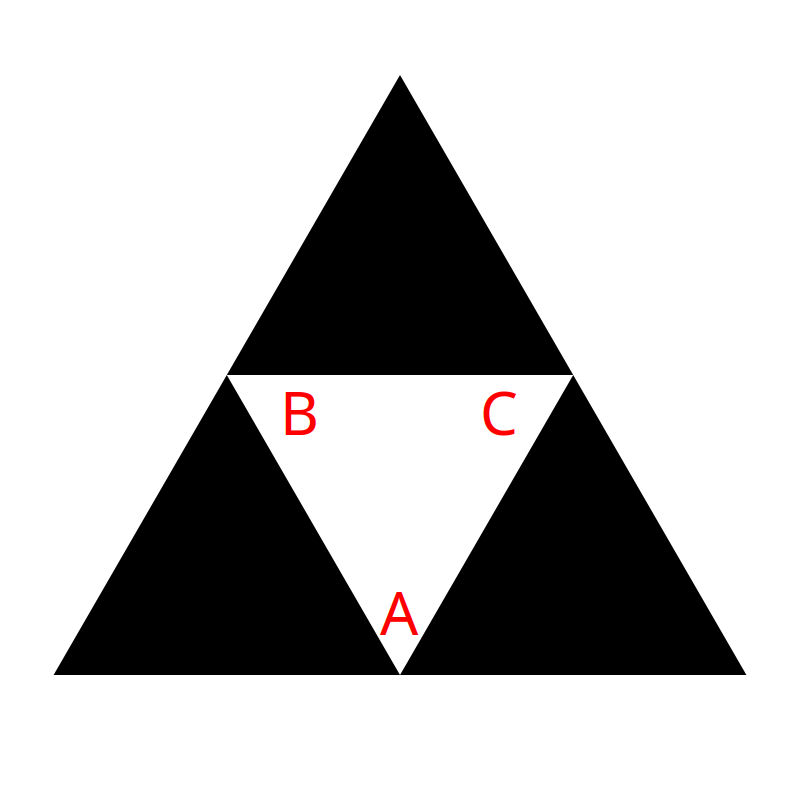
In the example we did above, we had A at the bottom. But let’s rotate the triangle 60 degrees clockwise so B is at the bottom like this:

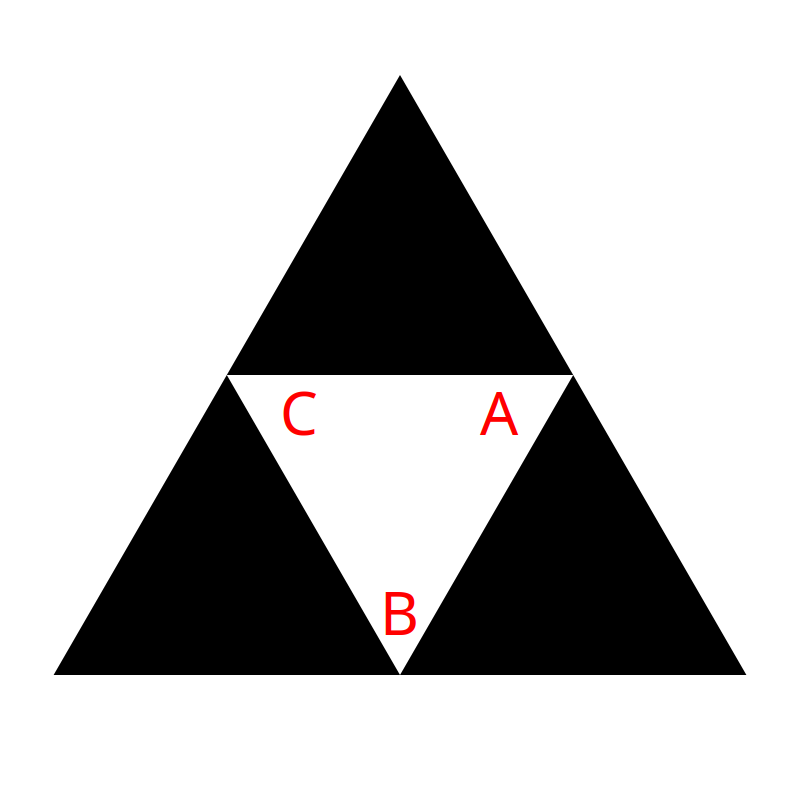
Removing the top triangle, one iteration looks no different.

But two iterations…

Three…

Four…

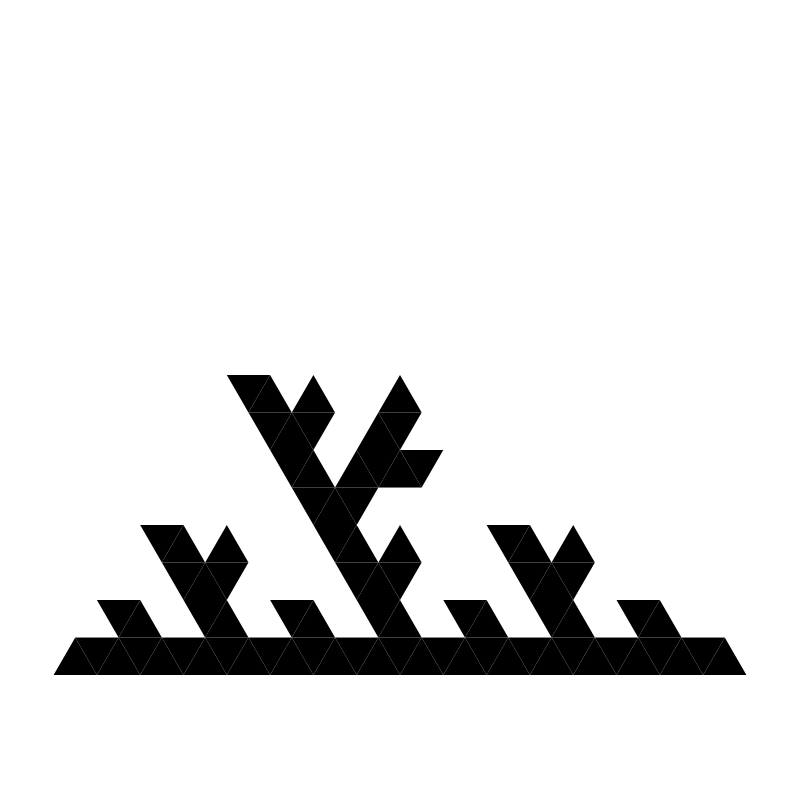
And finally…

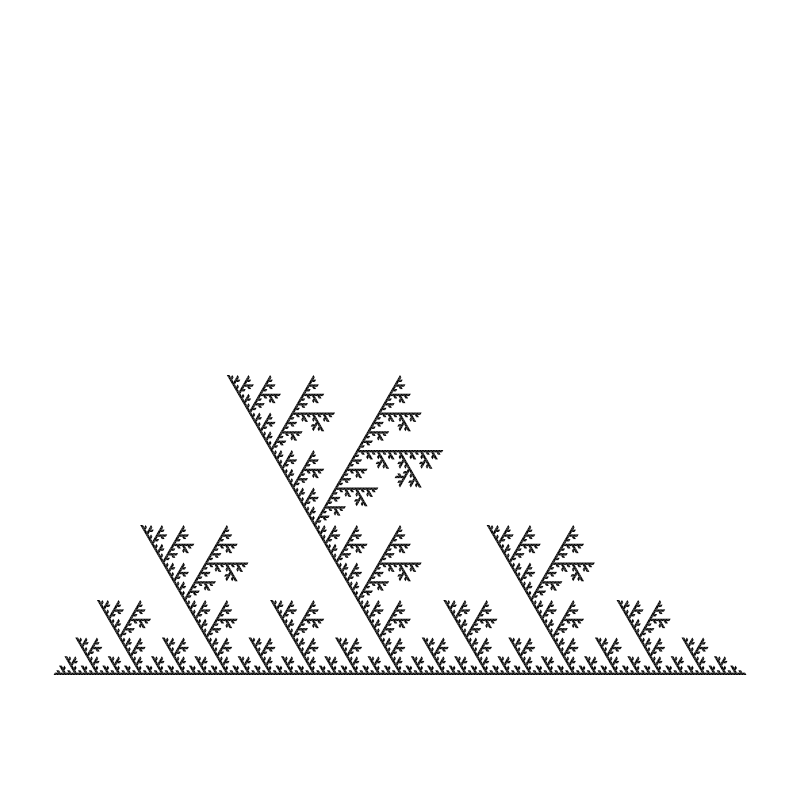
Now we’ve got something very different!

Now let’s do the same thing, but rotating the center triangle so C is at the bottom.

And removing the top triangle and rendering that all out…

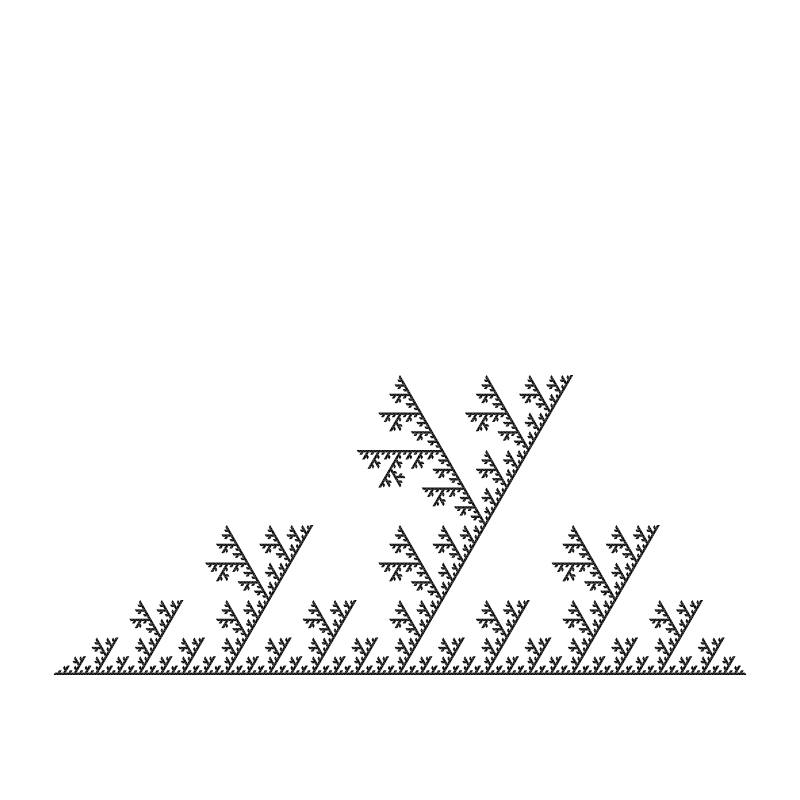
We have the same image, flipped.

Just to be clear, we can still remove the bottom right triangle (B) or bottom left (C) and we get the same image rotated:

Question Me

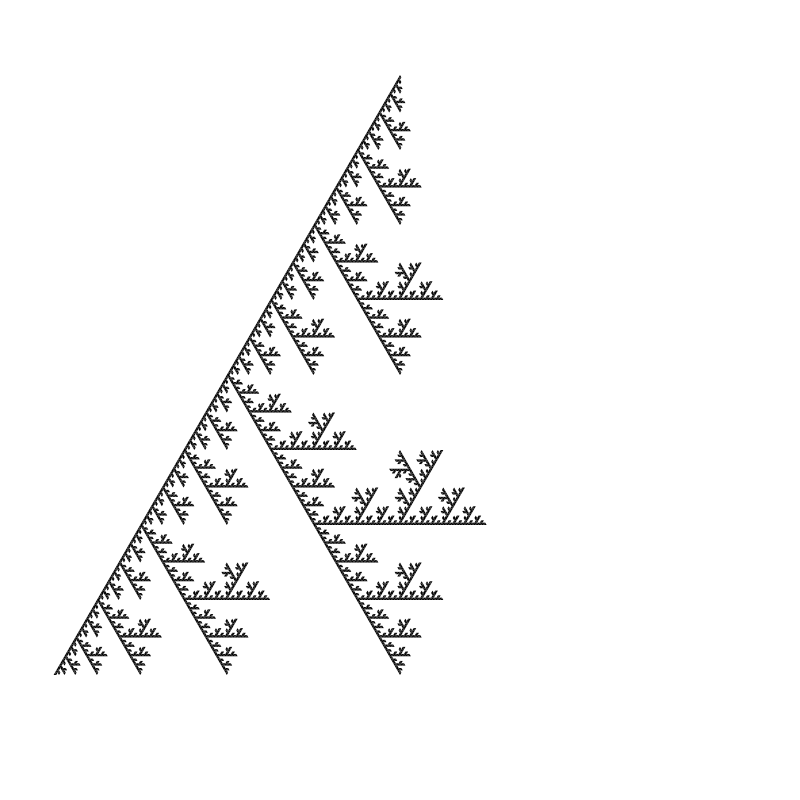
Earlier, I said when we had three choices on how to orient the center triangle, I lied.

There are three choices if we only rotate. But we can also mirror that triangle as we rotate it. Which gives us 3 more possibilities:

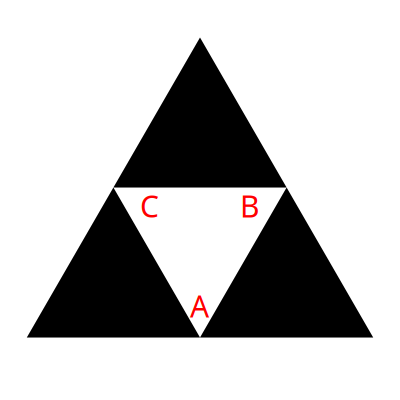
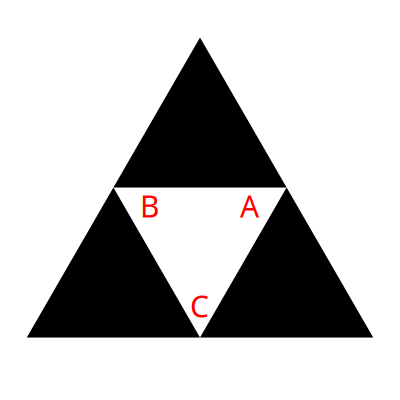
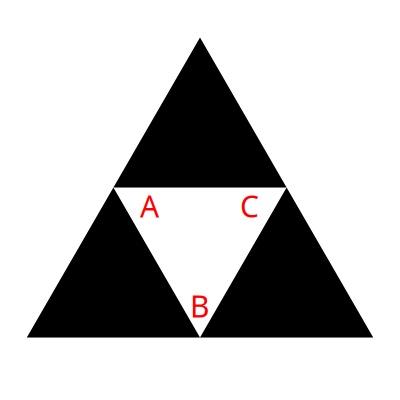
Let’s take the first one first, removing the top triangle.

No difference from what we originally had. Actually, it is flipped on the x-axis, but since it’s symmetrical, you can’t tell.

But when we remove the right or left triangles, we get something brand new.

Now we have a bunch of squashed Sierpinskis lined up. Neat!

What happens when we put B on the bottom?

Removing the top triangle…

Again we have infinite Sierpinskis lined up, but oriented differently and skewed a bit.

Bottom right…

Bottom left…

This one goes back to the original again.

Finally, for the sake of completeness, we’ll do the same with C on the bottom, removing top, bottom right, bottom left:

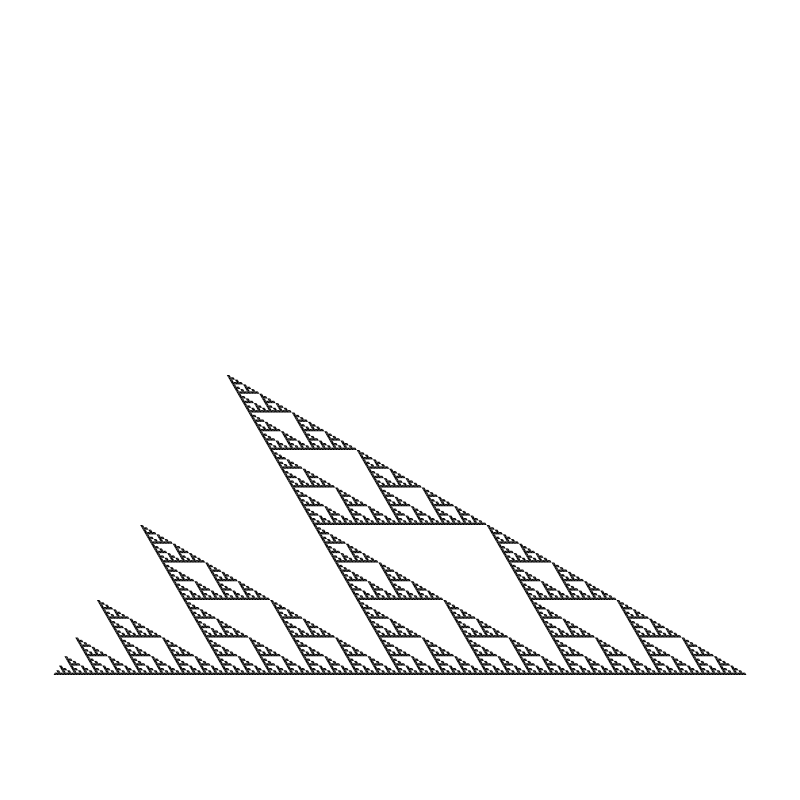
All the same, but differently oriented.

OK, we got all six orientations of the center triangle covered. So we’re all done, right?

Not even close!

Question Harder!

What about each of those three outer triangles? So far we’ve been orienting them all the same as the original: A on top, B on the bottom right, C on the bottom left.

But each one of those could be oriented in six different ways. That’s four triangles, each of which could be oriented six ways. 6x6x6x6, or 1296 possible variations!

Not to mention the fact that you can choose which triangle to remove - A, B or C, which triples the possibilities. Of course, many of the iterations will be the same as others, some just mirrored or rotated a bit differently, but there are still quite a few interesting ones.

I’m not going to go through all of them, but here’s a few neat ones I found:

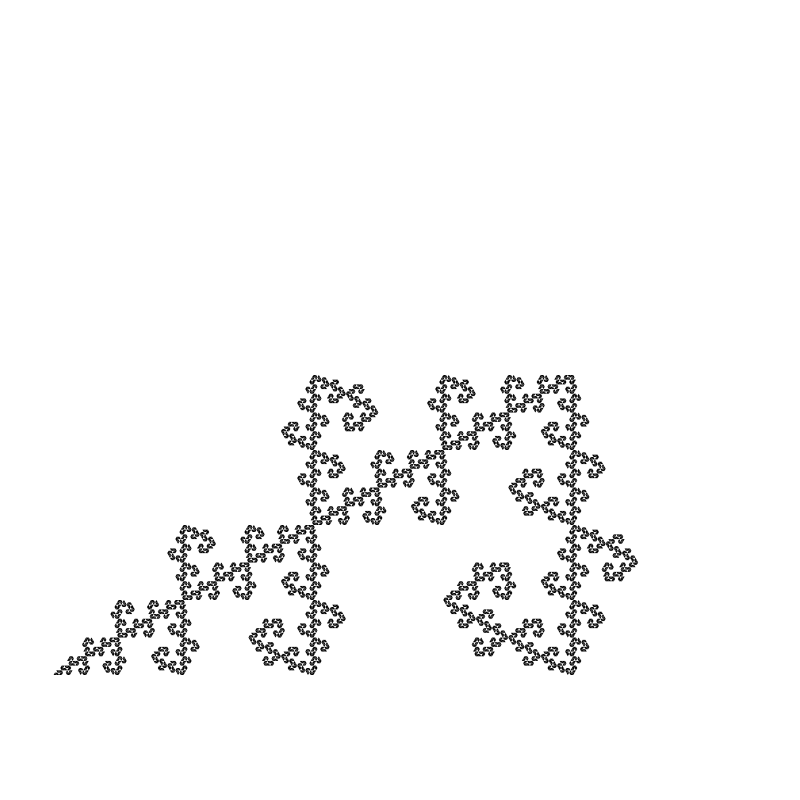
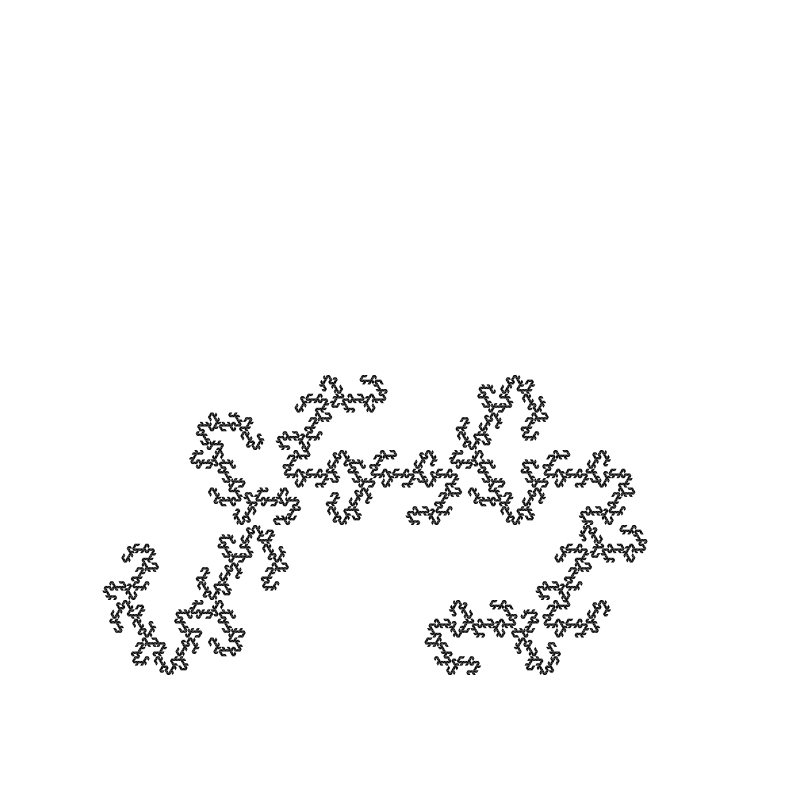
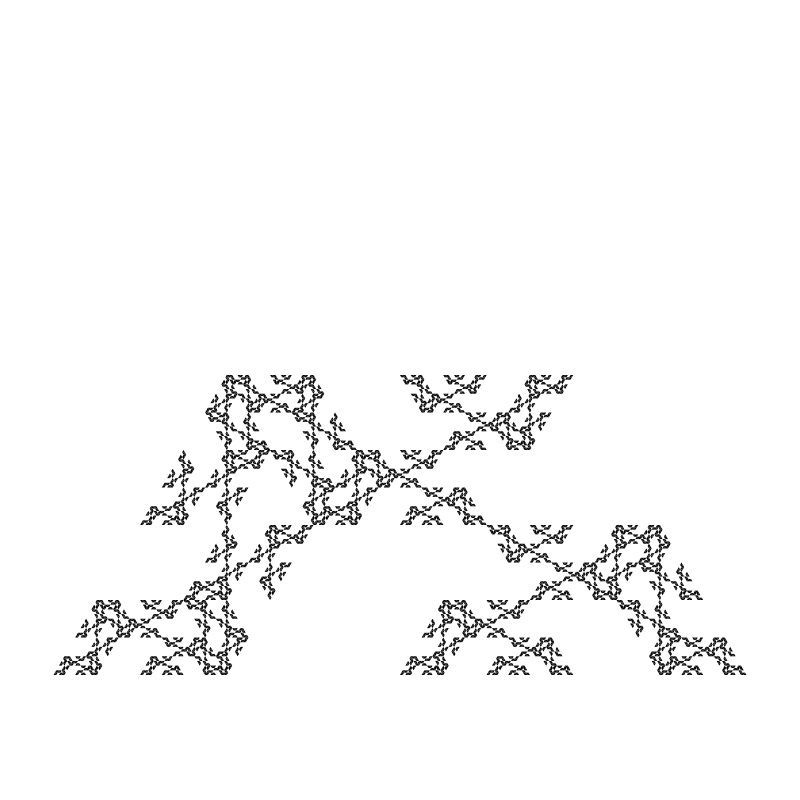
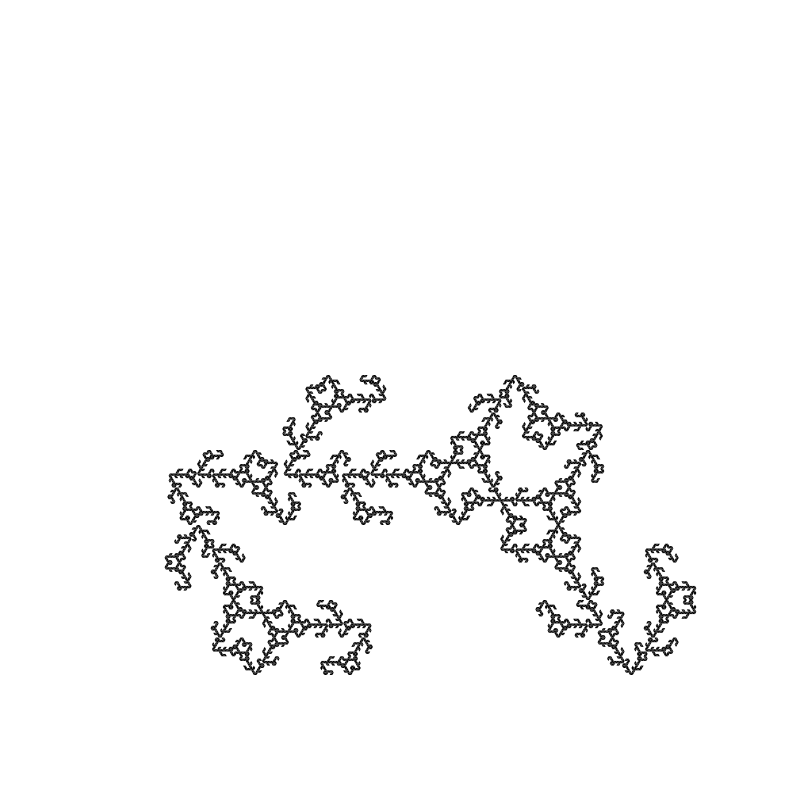
Some of these are looking curiously like Julia fractals!

Question the Question

Everything is too stable. We’re always removing the same triangle throughout all the iterations of an image. I took just ONE of the examples from the above list and altered it so that on each iteration, it randomly decides which triangle to remove.

And that’s only the start. You could randomly choose which order each triangle is in - in each iteration. Or not randomly - do it according to some scheme. I feel like I’ll be exploring this one for a while.

Question the End

After posting, I kept finding more nice looking ones. Here’s a few more.

---

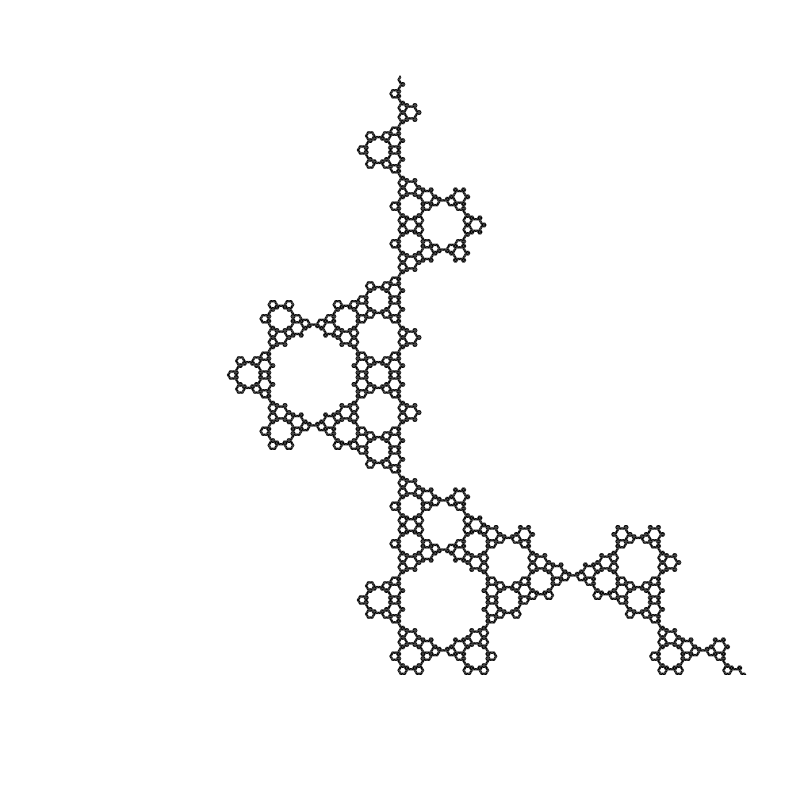
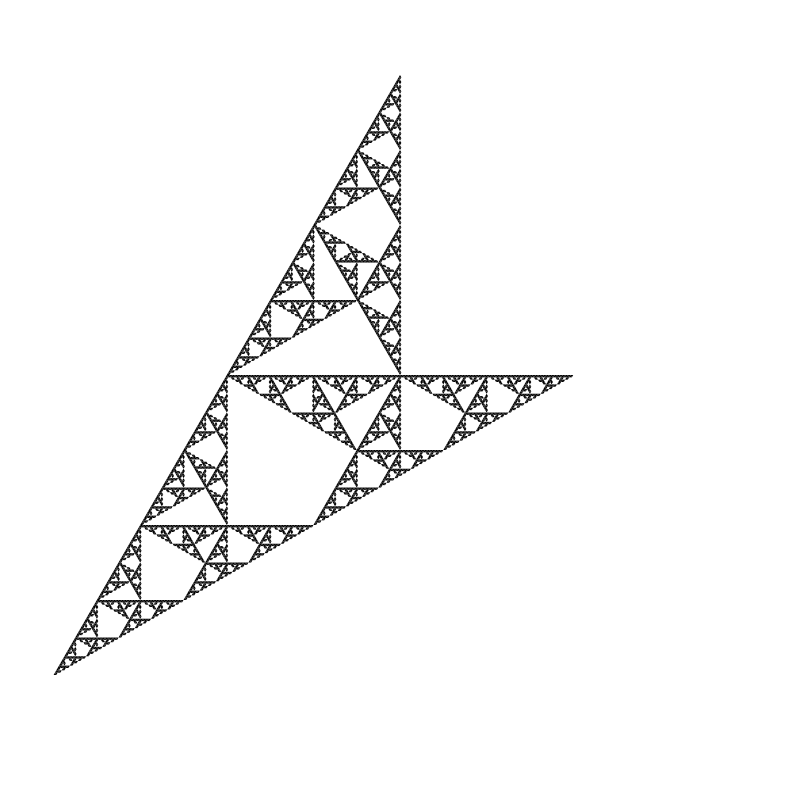
Comments? Best way to shout at me is on Mastodon

Or share this post directly on Mastodon